１５．三角形の内外の点と線と内分・外分 - 空・殻・核 (くうからかく）

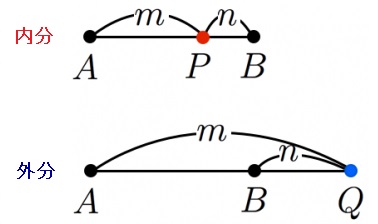
線分をまるでゴムのひものように考えると、それをm：nの比に分けるとき、その分割点をどこでつまんで実現するかによって「内分」か「外分」かが区別される。線分ABの内部のある点Pでつまむとき、線分ABをAP：PB＝m：nの比に内分するという。一方、線分ABの延長線上のある点Qでつまむとき、線分ABをAQ：QB＝m：nの比に外分するという。

f:id:hewhomeyouit:20190402082140j:plain — 図15-1　内分と外分

こうした比というものは、古くから探究されてきた。例えば、ユークリッドの『原論』の中で、「線分を一点で分け、長い部分と短い部分との比が、全体と長い部分との比に等しくなるようにしたときの比」という「外中比」というものが出て来る。これは、近代以降に「黄金比」と呼ばれるようになったものである。

さて、ここで、三角形の内部と外部の1点と、3辺に対する内分・外分の比に興味深い関係がある。また、それと同様に、三角形の内部を横断する直線、あるいは横断せずに外部を通る直線と、3辺に対する内分・外分の比にも興味深い関係がある。前者は「チェバの定理」、後者は「メネラウスの定理」と呼ばれる。

これらは、言葉だけで説明するより、実際に図を描いた方が一目瞭然の図式である。まず、三角形△ABCの3頂点A,B,Cや3辺BC,CA,ABといった三角形の境界線上にない三角形の内部の1点をSとするとき、3頂点A,B,Cと点Sを結ぶ直線AS,BS,CSと対辺BC,CA,ABとの交点をP,Q,Rとする。このとき、この3つの点P,Q,RがBC,CA,ABをそれぞれBP:PC＝a1:a2,CP:PA＝b1:b2,AP:PB＝c1:c2と内分するものとすれば、これら3辺の内分比の積はちょうど＋1になる。同様に、三角形△ABCの外部にある1点をSとするとき、3頂点A,B,Cと点Sを結ぶ直線AS,BS,CSと対辺BC,CA,ABもしくはそれらの延長線との交点をP,Q,Rとする。このとき、この3つの点P,Q,RがBC,CA,ABもしくはそれらの延長線分をそれぞれBP:PC＝a1:a2,CP:PA＝b1:b2,AP:PB＝c1:c2と内分もしくは外分するものとすれば、これら3辺の比の積はちょうど＋1になる。なお、比の符号は、三角形の3辺を反時計回りに回る方向を正とし、そうでない方向を負として計算する。

チェバの定理

(1)三角形の内部に点がある場合

f:id:hewhomeyouit:20190402082303j:plain — 図15-2　チェバの定理と内分・外分(1)

(2)三角形の外部に点がある場合

f:id:hewhomeyouit:20190402082359j:plain — 図15-3　チェバの定理と内分・外分(2)

メネラウスの定理

(1)三角形の内部を直線が通る場合

f:id:hewhomeyouit:20190402082642j:plain — 図15-4 メネラウスの定理と内分・外分(1)

(2)三角形の外部を直線が通る場合

f:id:hewhomeyouit:20190402082735j:plain — 図15-5　メネラウスの定理と内分・外分(2)

以上、三角形の内外の1点と、3辺もしくは1辺と2辺の延長線分の関係が「チェバの定理」であるが、小難しく感じる人のためにもう少し日本語でまとめておく。

三角形の内部に1点があるとき、それと3頂点を結ぶ線分はそれぞれ3辺を内分するが、その3つの比の値の積は＋1になる。三角形の外部に1点があるとき、それと3頂点を結ぶ線分は1辺を内分し、2辺を外分するが、その3つの比の値の積もまた＋1になる。

続いて、三角形△ABCの内部を直線ℓが横断するとき、この直線が、3辺BC,CA,ABもしくはそれらの延長線分と交わる交点をP,Q,Rとする。このとき、この3つの点P,Q,RがBC,CA,ABをそれぞれBP:PC＝a1:a2,CP:PA＝b1:b2,AP:PB＝c1:c2と分けるとすれば、これら3辺の内分比の積はちょうど－1になる。同様に、三角形△ABCの外部を直線ℓが通るときは、3辺BC,CA,ABの延長線分と交わる交点をP,Q,Rとすれば、この3つの点P,Q,RがBC,CA,ABをそれぞれBP:PC＝a1:a2,CP:PA＝b1:b2,AP:PB＝c1:c2と分けるとすれば、これら3辺の外分比の積はちょうど－1になる。

以上、三角形の内外の直線と、2辺と1辺の延長線分もしくは3辺の延長線分の関係が「メネラウスの定理」であるが、これも小難しく感じる人のためにもう少し日本語でまとめておく。

三角形の内部を直線が横断するとき、その直線は2辺を内分し、残り1辺を外分するが、その3つの比の値の積は＋1になる。また、三角形の外部を直線が通るときは、その直線と3辺の延長線分との交点で外分するが、その3つの比の値の積もまた－1になる。

最後に、きちんとまとめ直せば、以下の通りである。

【チェバの定理】

(1)三角形の内部に点がある場合

△ABCの内部に共点Sがある（AP,BQ,CRは共通の交点Sを持つ）

⇔BCを内分する点P,CAを内分する点Q,ABを内分する点R（3辺の内分点）

BP/PC・CQ/QA・AR/RB＝＋1

(2)三角形の外部に点がある

△ABCの外部に共点Sがある（AP,BQ,CRは共通の交点Sを持つ）

⇔BCを内分する点P,CAを外分する点Q,ABを外分する点R（1辺の内分点,2点の外分点）

BP/PC・CQ/QA・AR/RB＝＋1