１９．自然な数の拡張と複素数

私たち人間にとって最も親しみのある数と言えば、1,2,3,…という自然数である。そもそも数は、人間がある対象を1つの単位（ユニット）として「1」として閉じて「認識」することから始まり、それと同一視するところから「2」「3」と順に閉じて認識していくことこそ「数える」という行為である。

人間はこの数同士を関係づける行為として「計算する」ということを行ってきた。最も基本的な計算は「足し算」（加法）だ。自然数同士の足し算の結果も自然数になる。人間は行ったら帰るという行き来というか往復というセンスを持っていて、足したら、今度は引いて戻ってくる計算を行いたくなる。これが「引き算」（減法）という足し算の逆計算だが、自然数同士の引き算は必ずしも計算結果は自然数にならないことがある。例えば、ｍ－ｎという引き算において、引かれる数ｍと引く数ｎが同じ場合は計算結果は０（ゼロ）になるし、引かれる数ｍより引く数ｎの方が大きいと計算結果は自然数に－符号を付けた数になっる。自然数に－符号を付けた数を負の整数と呼ぶ。一方自然数は、正の整数と呼ぶ。この正の整数、０、負の整数を合わせて、「整数」と呼ぶ。

この整数同士は足し算（加法）や引き算（減法）や掛け算（乗法）を行っても整数になる。しかし、整数を（０を除く）整数で割り算（除法）をしても、割り切れない場合は整数にならない。割り切れない場合は分数の形で書ける。このようなものは整数も含めて「有理数」と呼ぶ。ここまで、数の集合を、自然数→整数→有理数まで拡張したが、ここまでだと「連続性」を有する形である「直線」上の点を対応付けることはできない。例えば、同じ数同士を掛け合わせて2となる数といった数は有理数にはならない。このような数を「無理数」と呼ぶ。有理数と無理数を合わせて、「実数」と呼ぶ。実数は実数同士で足し算・引き算・掛け算・割り算という加減乗除の計算（四則演算）を行っても実数になる。

数学では、このような「数」と同様の特性を他の形式の元を持つ集合にも適用して、数と同様の扱いをしたいと考える。要するに、数と全く同じではないが、数と似たような計算ができる集合というものを考える。これが「群」「環」「体」といった代数学的な構造を持つ集合である。このうち、最も基本的なものが「群」である。群の詳しい定義はここでは述べない。

以上までの数の集合について、以下にざっくりまとめてみる。

・自然数…加法・乗法ができる。ただし、加法における単位元・逆元や、乗法における逆元は持てない。また、自然数の指数による冪（累乗）も計算できるが、逆元は持てない。

{1, 2, 3, ……}

・整数……加法・乗法・減法ができる。「零元」（加法における単位元）として「0」、「反数」（加法における逆元）として「負の整数」を持てる。→加法群という「群」として閉じる。また、自然数の指数による冪（累乗）も計算できるが、逆元は持てない。直線上では「離散」性を持つ。

{…－3, －2, －1, 0, 1, 2, 3, ……}

・有理数…加法・乗法・減法・除法（0による除法は除く）ができる。「逆数」（加法における逆元）を持てる。→加法群・乗法群として閉じる。つまり、「環」として閉じる。また、整数の指数による冪（累乗）も計算できる。直線上では「稠密」性を持つ。

{…－3, －2, －1, 0, 1, 2, 3, …, 1/2, 2/3, －3/4, －5/2, …}

・実数……加法・乗法・減法・除法（0による除法は除く）ができる。

冪（累乗）の逆演算ができ、「冪根」（冪（累乗）における逆元）を持てる。「無理数」として、平方根や立方根などの「冪根」以外にも、円周率πや、ネイピア数（自然対数の底）eなどを持てる。また、実数の指数による冪（累乗）も計算できる。直線上では「連続」性を持つ。

{…－3, －2, －1, 0, 1, 2, 3, …, 1/2, 2/3, －3/4, －5/2, …, √2, e,π, …}

既知の数（定数）と未知の数（変数）の掛け算もまた変数となる。この変数はそのとる値の範囲の分だけ「自由」度を持つ。この変数がある定数と一致するという「拘束」条件を与える。こうすれば、特定の「問い」が成り立つ。この「問い」に対する「答え」を求める。これが「方程式」というものである。

最も簡単な方程式は、以下の1次方程式である。

図19-1　1次方程式

この定数係数a,bが有理数までなら、この解は必ず有理数であり、この定数係数a,bが実数までなら、この解は必ず実数である。

次に、以下のように2次方程式というものもある。

図19-2　2次方程式

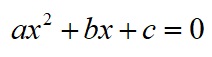
これを拡張して、n次方程式を考えることができる。

図19-3　n次方程式

普通、n次方程式の基本定理として（重複解を含めて）n個の解を持つ。つまり、2次方程式は（重複解を含めて）2個の解を持つということだ。ところが、解の範囲が実数までだと、解を2個持たない場合が存在する。

例えば、最も簡単な2次方程式

図19-4　－1の平方根を求める2次方程式

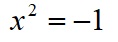
といういわゆる－1の平方根を求める方程式は、実数の範囲では解なしとなる。ここで、無理やり数の集合の範囲を、実数から拡張して「負の実数の平方根」を許容して「虚数」というものを認めると、解を2個持つようになる。この－1の平方根の正の方を「虚数単位」と呼び、iと書く。

つまり、

図19-5　－1の平方根

と定義する。「負の実数の平方根」を、特に「純虚数」と呼ぶ。

ここで、「負の実数の平方根」を許容するという行為こそ、数に具体的なものを求めるだけでなく、より抽象度の高い構造を持ったものを「数」として認めたことになる。この結果、数は感覚的に認識できる存在から、思考的な存在として認識できるレベルにまでなったのである。

こうして、2次方程式は必ず解をもち、実数でない解は、

図19-6　複素数の形式

という形式で書ける数となる。ただし、αとβは実数である。このαが実数部分であり、βiが虚数部分である、この実数と虚数を＋記号で結んだものを数と認め、「複素数」と呼ぶ。こうして、複素数というものが数として導入された。以上で、複素数がこれまでの実数までの数の拡張とはちょっと違った形式のものであることがわかった。

よく考えてみれば、自然数→整数→有理数という拡張は、加減乗除という四則演算を成り立たせるための拡張であった。そして、1次方程式の解はここまでの数の拡張で求まる。次の実数への拡張は、平方根を求めたりする、2次方程式の解を求めることとも関係するが、それでは完全ではなく、直線上の点と対応付ける連続性を要請すると、円周率πやネイピア数eといった「超越数」をも含めるようになる。超越数とは、普通の（代数的な）方程式の解ではないような実数である。2つの実数同士は、大小関係を比較できる。一般に、実数は、整数、有限小数、循環小数、循環しない小数のいずれかで表現できる。

一方、複素数は大小関係を比較しようのない数であり、長い間、自然界の何らかの存在と直接対応付けるようなものはないと考えられてきた。ところが、実際には、波動の形式的な解として用いられ、電磁気学にも応用された。だが、これらはまだ数学的計算上便利な形式的な解として用いられるのがせいぜいであった。ところが、量子力学という分野が立ち上がってきたとき、量子という存在自体が、それが存在する条件として、複素数以上の構造を持つ概念が必要とされるようになった。それは量子力学における物理量が単なる実数に留まらず、少なくとも複素数以上の構造を要する、ある意味では実在的な量の根拠として紐づけられるものであることがわかったわけである。